| パソコンを使った1次関数 | |
| grapesを使った一次関数の授業で使ったテキストです | |
| パソコンを使って一次関数について学習しよう | |
| | |
| 1 コンピュータの電源を入れてください。 | |
 | |
| 2 「grapes」のアイコン(ぶどう)ダブルクリックする。 3 「開く」アイコンをクリック(ファイル・開くでもよい)する | |
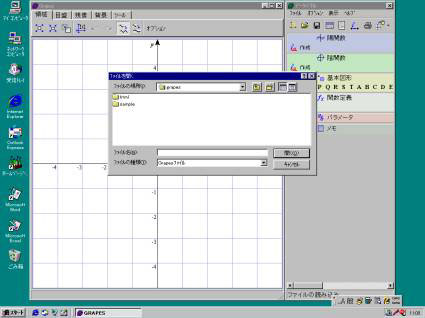 | |
| 4 「sample」を選んでクリックする | |
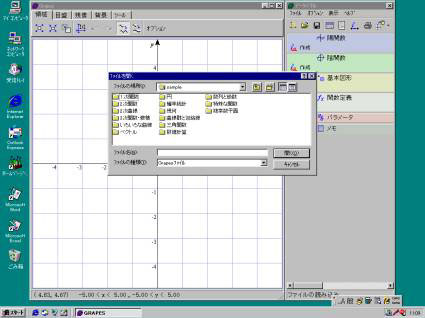 | |
| 5 「1次関数」を選びクリックする | |
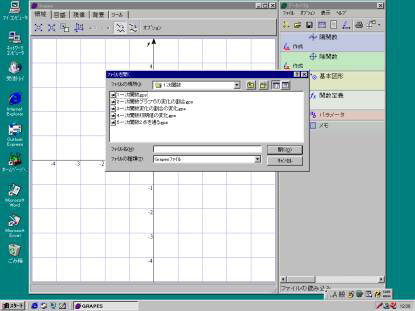 | |
| 6 「1一次関数」を選んで、「開く」をクリックする | |
| 初期値bと変化の割合aの値を入力しグラフ上での様子を見ましょう | |
| 入力xが−5から5まで変化するときの様子をみます | |
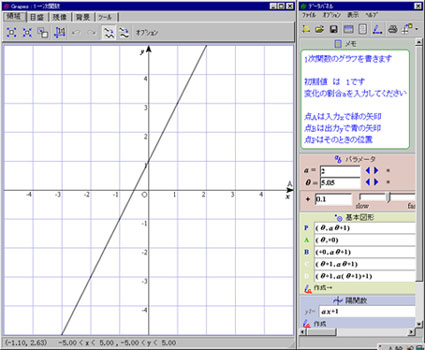 | |
| 初期値は 1 です | |
| (ア) 変化の割合aに 0.5 を入力してください 出力yは ?@増えている ?A減っている ?B変わらない (イ) 変化の割合aに 2 を入力してください 出力yは ?@増えている ?A減っている ?B変わらない 点Bの動きは 0.5 のときより ?@早い ?A遅い (ウ) 変化の割合aに −1.5 を入力してください 出力yは ?@増えている ?A減っている ?B変わらない (エ) 変化の割合aが −0.25 を入力してください 出力yは ?@増えている ?A減っている ?B変わらない 点Bの動きは -1.5 のときより ?@早い ?A遅い (オ) 変化の割合aが 0 出力yは ?@増えている ?A減っている ?B変わらない 質問 出力yの増減について
| |
| 7 「開く」アイコンをクリックする 「2一次関数グラフでの変化の割合」を選んで、「開く」をクリックする | |
| | |
| 初期値bと変化の割合aの値を入力しグラフ上での変化の割合を見ましょう | |
| 入力xが−5から5まで変化するときの様子をみます | |
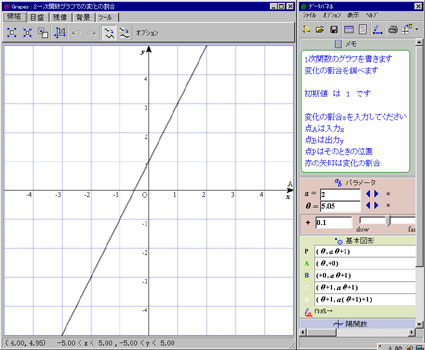 | |
| 初期値は 1 です | |
| (ア) 変化の割合aが 0.5 のとき 変化の割合を表す矢印は 1上向き 2下向き 3ない イ) 変化の割合aが 2 のとき 変化の割合を表す矢印は 1上向き 2下向き 3ない (ウ) 変化の割合aが −1.5 のとき 変化の割合を表す矢印は 1上向き 2下向き 3ない (エ) 変化の割合aが −0.25 のとき 変化の割合を表す矢印は 1上向き 2下向き 3ない (オ) 変化の割合aが 0 のとき 変化の割合を表す矢印は 1上向き 2下向き 3ない 質問 変化の割合を表す矢印は、どんなときに上を向き、どんなときに下を向き、どんなときになくなります | |
| 8 「開く」アイコンをクリックし 「3一次関数グラフでの変化の割合の変化」を選んで、「開く」をクリックする | |
| 初期値bと変化の割合aの値を入力しグラフ上での変化の割合を見ましょう | |
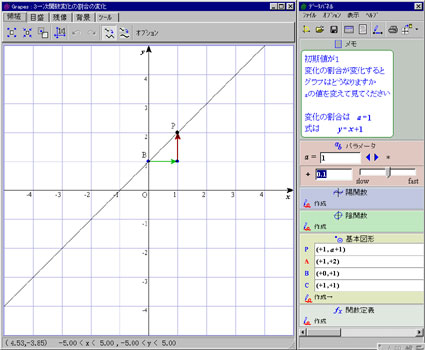 | |
| 現在 初期値が 1、 変化の割合が 1 です。 式は y=x+1 です。 | |
| 変化の割合を変えるとグラフはどう変わるかを調べましょう 1 「変化の割合」aの値を大きくすると、グラフはどんな変化をしますか 2 「変化の割合」aの値を小さくすると、グラフはどんな変化をしますか 3 「変化の割合」a がプラスのとき、グラフは「右上がり」ですか、「右下がり」ですか 4 「変化の割合」a がマイナスのとき、グラフは「右上がり」ですか、「右下がり」ですか 5 どうして1や2のようになるのですか | |
| 9 「開く」アイコンをクリックし 「4一次関数初期値の変化」を選んで、「開く」をクリックする | |
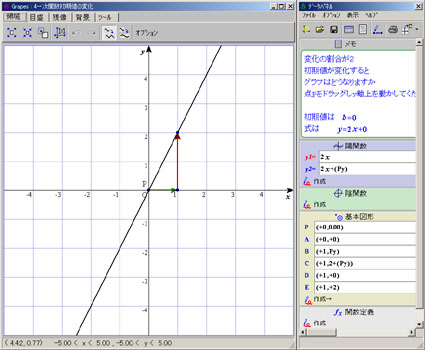 | |
| 現在 初期値が 0、 変化の割合が 2 です。 式は y=2x+0 つまり y=2x です。 | |
| 初期値を変えるとグラフはどう変わるかを調べましょう マウスを動かし「+」を点Pまで移動すると「手でつかむ」形に変わります 1 マウスの左を押したままy軸の上の方向に動かします(「ドラッグ」といいます) グラフはどんな変化をしましたか 2 マウスの左を押したままy軸の下の方向に動かします グラフはどんな変化をしましたか 3 どうしてこのような変化をするのですか | |
| 10 「開く」アイコンをクリックし 「5一次関数2点を通る」を選んで、「開く」をクリックする | |
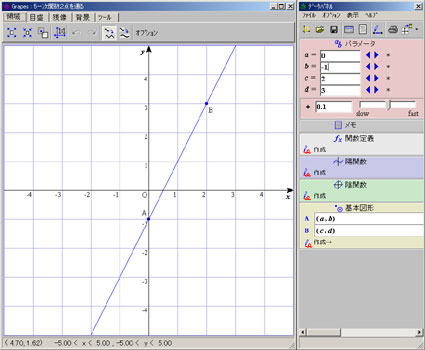 | |
| いま 入力 x=a のとき 出力 y=b 入力 x=c のとき 出力 y=d つまり 点A(a,b), 点B(c,d) です 1 点A(0,−1) 点B(2,3) とします したがって a=0,b=−1,c=2,d=3 と入力してください。 出来上がったグラフを見て (初期値)= (変化の割合)= (1次関数の式) を求めてください。 2 点A(1,−1) 点B(−1,3) とします したがって a=1,b=−1,c=−1,d=3 と入力してください。 出来上がったグラフを見て (初期値)= (変化の割合)= (1次関数の式) を求めてください。 3 点A(0,4) 点B(3,2) とします したがって a=0,b=4,c=3,d=2 と入力してください。 出来上がったグラフを見て (初期値)= (変化の割合)= (1次関数の式) を求めてください。 4 点A(1,1) 点B3,5) とします したがって a=1,b=1,c=3,d=5 と入力してください。 出来上がったグラフを見て (初期値)= (変化の割合)= (1次関数の式) を求めてください。 5 点A(1,2) 点B(4,3) とします したがって a=1,b=2,c=4,d=3 と入力してください。 出来上がったグラフを見て (初期値)= (変化の割合)= (1次関数の式) を求めてください。 6 点A(−2,−1) 点B(3,2) とします したがって a=−2,b=−1,c=3,d=2 と入力してください。 出来上がったグラフを見て (初期値)= (変化の割合)= (1次関数の式) を求めてください。 | |
| 11 「開く」アイコンをクリックし 「6一次関数と変域」を選んで、「開く」をクリックする。 | |
| 一次関数 y=ax+b について xの変域が c<x<d のときの yの変域を求めてみましょう。 c,d,bの順に入力し、最後にaを入力すると xがx軸上をcからdまで変化していきます。 そのとき、yはy軸上を変化していきます。 そのときの、赤の矢線がyの変域です。 1 一次関数 y=x−2 について xの変域が 1<x<3 のときのyの変域を求めてください。 ここで、つぎの順序でa,b,c,dの4つの値を入力してください。 cに1を入力してください dに3を入力してください 初期値bに−2を入力してください 最後に変化の割合aに1を入力してください。 xがx軸上を1から3まで変化するとき、yはy軸上で変化していきます。 赤の矢線がyの変域です。 したがって、yの変域は <y< となります。 2 一次関数 y=0.5x−1 について xの変域が −4<x<−2 のときのyの変域を求めてください。 ここで、つぎの順序でa,b,c,dの4つの値を入力してください。 cに−4を入力してください dに−2を入力してください 初期値bに−1を入力してください 最後に変化の割合aに0.5を入力してください。 xがx軸上を−4から−2まで変化するとき、yはy軸上で変化していきます。 赤の矢線がyの変域です。 したがって、yの変域は <y< となります。 3 一次関数 y=−x+2 について xの変域が 1<x<4 のときのyの変域を求めてください。 ここで、つぎの順序でa,b,c,dの4つの値を入力してください。 cに1を入力してください dに4を入力してください 初期値bに2を入力してください 最後に変化の割合aに−1を入力してください。 xがx軸上を1から4まで変化するとき、yはy軸上で変化していきます。 赤の矢線がyの変域です。 したがって、yの変域は <y< となります。 4 一次関数 y=−3x−4 について xの変域が −3<x<−2 のときのyの変域を求めてください。 ここで、つぎの順序でa,b,c,dの4つの値を入力してください。 cに−3を入力してください dに−2を入力してください 初期値bに−4を入力してください 最後に変化の割合aに−3を入力してください。 xがx軸上を−3から−2まで変化するとき、yはy軸上で変化していきます。 赤の矢線がyの変域です。 したがって、yの変域は <y< となります。 5 一次関数 y=−2x+1 について xの変域が −1<x<3 のときのyの変域を求めてください。 ここで、つぎの順序でa,b,c,dの4つの値を入力してください。 cに−1を入力してください dに3を入力してください 初期値bに1を入力してください 最後に変化の割合aに−2を入力してください。 xがx軸上を−1から3まで変化するとき、yはy軸上で変化していきます。 赤の矢線がyの変域です。 したがって、yの変域は <y< となります。 | |